“Difficult circumstances serve as a textbook of life for people”

Deep Learning Principle

Standard Scaling

Standardization of a dataset is a common requirement for many machine learning estimators: they might behave badly if the individual features do not more or less look like standard normally distributed data (e.g. Gaussian with 0 mean and unit variance).
For instance many elements used in the objective function of a learning algorithm (such as the RBF kernel of Support Vector Machines or the L1 and L2 regularizers of linear models) assume that all features are centered around 0 and have variance in the same order. If a feature has a variance that is orders of magnitude larger that others, it might dominate the objective function and make the estimator unable to learn from other features correctly as expected.

Keras and Tensorflow

Keras as a simplified API to TensorFlow
Keras is a simple, high-level neural networks library, written in Python that works as a wrapper to Tensorflow[1] or Theano[2] . Its easy to learn and use.Using Keras is like working with Logo blocks. It was built so that people can do quicks POC’s and experiments before launching into full scale build process
TensorFlow is somewhat faster than Keras

Keras Function Input Explaination

Encoder

Mupltiple encoding techniques Intro: label, one-hot, vector, optimal binning, target encoding

All encoder methods !!! IMPORTANT

Summary:

Classic Encoders

The first group of five classic encoders can be seen on a continuum of embedding information in one column (Ordinal) up to k columns (OneHot). These are very useful encodings for machine learning practitioners to understand.

Ordinal — convert string labels to integer values 1 through k. Ordinal.

OneHot — one column for each value to compare vs. all other values. Nominal, ordinal.

Binary — convert each integer to binary digits. Each binary digit gets one column. Some info loss but fewer dimensions. Ordinal.

BaseN — Ordinal, Binary, or higher encoding. Nominal, ordinal. Doesn’t add much functionality. Probably avoid.

Hashing — Like OneHot but fewer dimensions, some info loss due to collisions. Nominal, ordinal.

Contrast Encoders

The five contrast encoders all have multiple issues that I argue make them unlikely to be useful for machine learning. They all output one column for each column value. I would avoid them in most cases. Their stated intentsare below.

Helmert (reverse) — The mean of the dependent variable for a level is compared to the mean of the dependent variable over all previous levels.

Sum — compares the mean of the dependent variable for a given level to the overall mean of the dependent variable over all the levels.

Backward Difference — the mean of the dependent variable for a level is compared with the mean of the dependent variable for the prior level.

Polynomial — orthogonal polynomial contrasts. The coefficients taken on by polynomial coding for k=4 levels are the linear, quadratic, and cubic trends in the categorical variable.

Bayesian Encoders

The Bayesian encoders use information from the dependent variable in their encodings. They output one column and can work well with high cardinality data.

Target — use the mean of the DV, must take steps to avoid overfitting/ response leakage. Nominal, ordinal. For classification tasks.

LeaveOneOut — similar to target but avoids contamination. Nominal, ordinal. For classification tasks.

WeightOfEvidence — added in v1.3. Not documented in the docs as of April 11, 2019. The method is explained in this post.

James-Stein — forthcoming in v1.4. Described in the code here.

M-estimator — forthcoming in v1.4. Described in the code here. Simplified target encoder.

Label encoding

Label encoding is simply converting each value in a column to a number, usually from test to numerical. For example, the body_style column contains 5 different values. We could choose to encode it like this:

convertible -> 0
hardtop -> 1
hatchback -> 2
sedan -> 3
wagon -> 4

DISADVANTAGE:

The numeric values can be “misinterpreted” by the algorithms. For example, the value of 0 is obviously less than the value of 4 but does that really correspond to the data set in real life? Does a wagon have “4X” more weight in our calculation than the convertible? I don’t think so.

One-hot encoding

convert each category value into a new column and assigns a 1 or 0 (True/False) value to the column. This has the benefit of not weighting a value improperly but does have the downside of adding more columns to the data set.

Target encoding

Target encoding is the process of replacing a categorical value with the mean of the target variable. In this example, we will be trying to predict bad_loan using our cleaned lending club data: https://raw.githubusercontent.com/h2oai/app-consumer-loan/master/data/loan.csv.

One of the predictors is addr_state, a categorical column with 50 unique values. To perform target encoding on addr_state, we will calculate the average of bad_loan per state (since bad_loan is binomial, this will translate to the proportion of records with bad_loan = 1).

For example, target encoding for addr_state could be:

addr_state	average bad_loan
AK	0.1476998
AL	0.2091603
AR	0.1920290
AZ	0.1740675
CA	0.1780015
CO	0.1433022

Instead of using state as a predictor in our model, we could use the target encoding of state.

Dummy Variables (one-hot encoding): One-hot encoding must apply in classifier

Use of Dummy Variables

Why one-hot encoding in classifier, not label encoding?

Because the disadvantage of label encoding: The numeric values can be “misinterpreted” by the algorithms. For example, the value of 0 is obviously less than the value of 4 but does that really correspond to the data set in real life? Does a wagon have “4X” more weight in our calculation than the convertible? I don’t think so.

This has the benefit of not weighting a value improperly but does have the downside of adding more columns to the data set.

Dummy Variable Trap:

The Dummy variable trap is a scenario where there are attributes which are highly correlated (Multicollinear) and one variable predicts the value of others. When we use one hot encoding for handling the categorical data, then one dummy variable (attribute) can be predicted with the help of other dummy variables. Hence, one dummy variable is highly correlated with other dummy variables. Using all dummy variables for regression models lead to dummy variable trap. So, the regression models should be designed excluding one dummy variable. (say, we have three, remove one of them)

ANN training step

Activation Functions

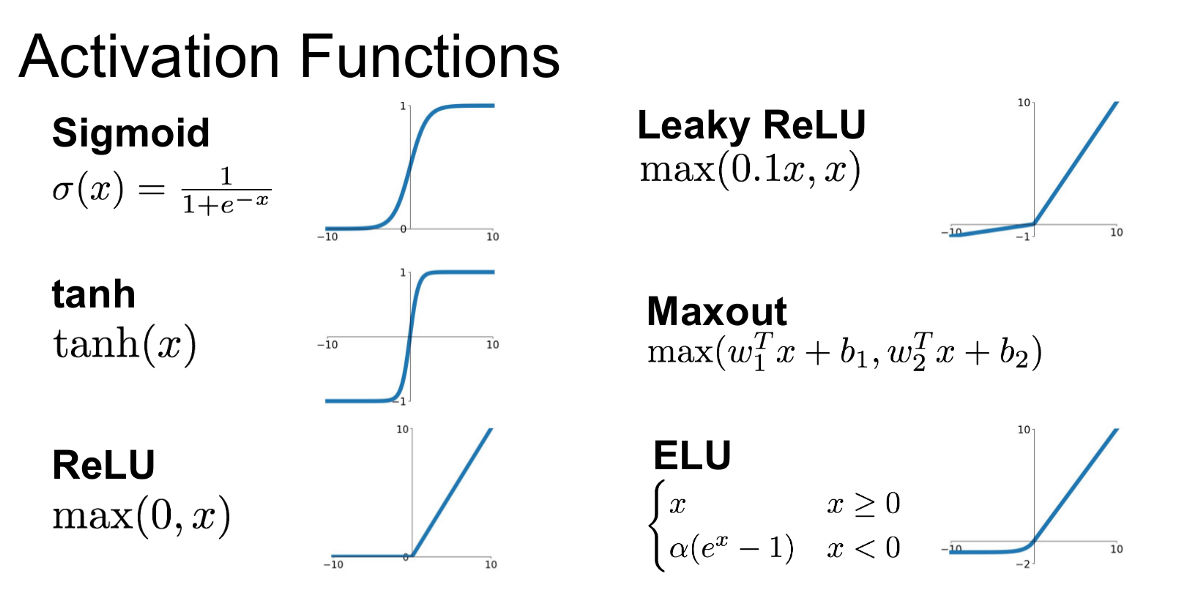
Rectifier (“I want to see only what I am looking for”)

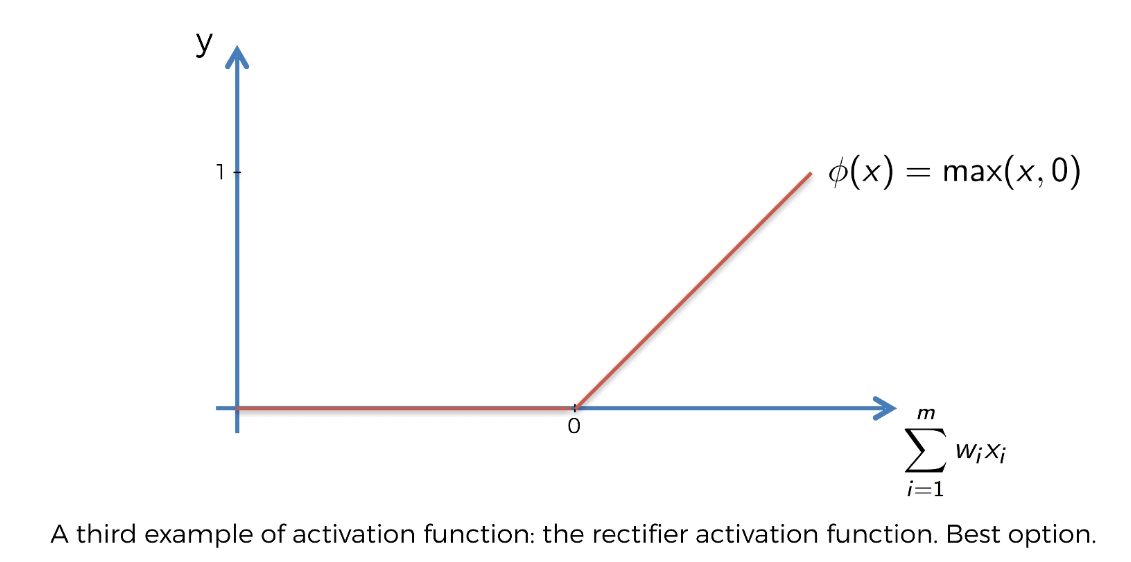
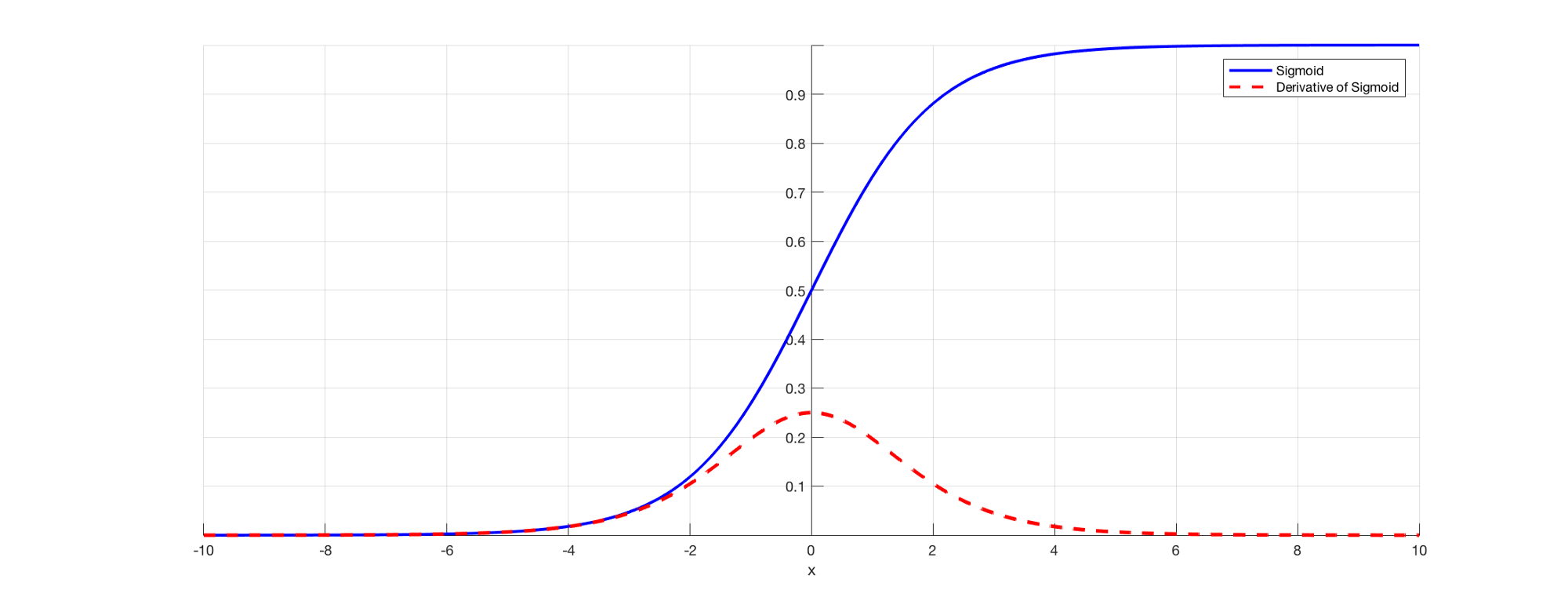
Sigmoid

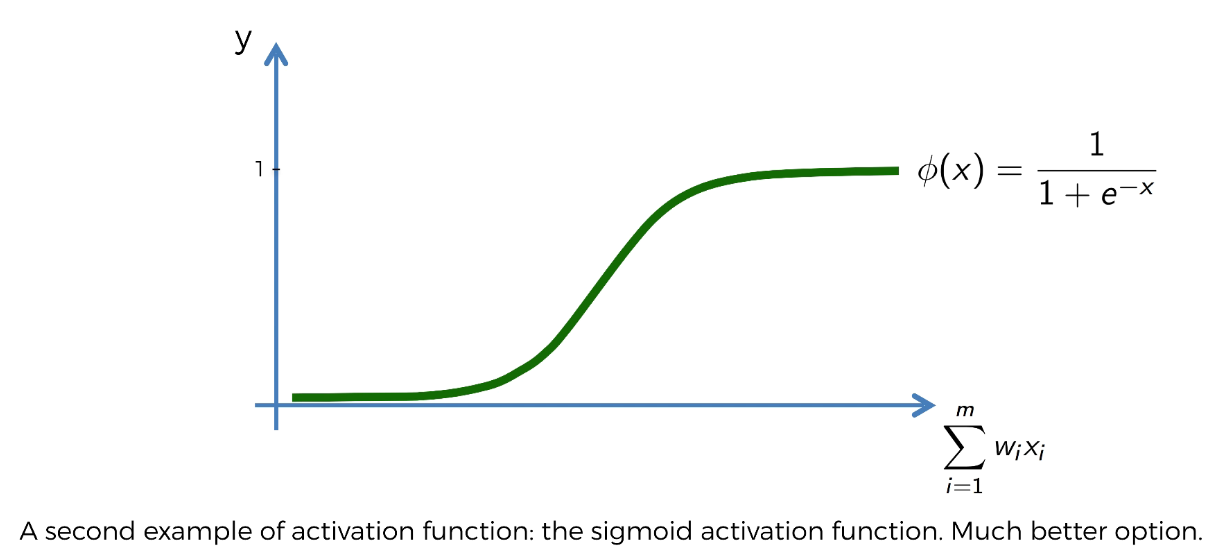
Softmax (Also known as “give-me-the-probability-distribution” function)

Example

Formula

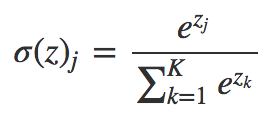
Keras

Dense(): Choose number of nodes in the hidden layer

units = avg(# of nodes in the input layer, # of nodes in the output layer)

in which, 11 predictors and 1 response variable => (11+1)/2 => 6

Choose activation function:

Activation function cheetsheet

Both sigmoid (kill gradients; slow converage (vanishing gradient); ok in the last layer) and tanh functions are not suitable for hidden layers (and avoid them) because if z is very large or very small, the slope of the function becomes very small which slows down the gradient descent which can be visualized in the below video.
Rectified linear unit (relu) is a preferred choice for !!all hidden layers!! because its derivative is 1 as long as z is positive and 0 when z is negative. In some cases, leaky rely can be used just to avoid exact zero derivatives (dead neurons but avoid overfitting).
Softmax: Use in output layer for classification In the case of multiclass specification, the actual class you have predicted will assemble in a value close to 1. And all other classes are assembled in values close to 0
Linear: Use in output layer for regression

Loss Functions: ?????????????

Cross-Entropy: Classification the decision boundary in a classification task is large (in comparison with regression)

MSE: Regression

Gradient vanishing

Certain activation functions, like the sigmoid function, squishes a large input space into a small input space between 0 and 1. Therefore, a large change in the input of the sigmoid function will cause a small change in the output. Hence, the derivative becomes small. For instance, first layer will map a large input region to a smaller output region, which will be mapped to an even smaller region by the second layer, which will be mapped to an even smaller region by the third layer and so on. As a result, even a large change in the parameters of the first layer doesn’t change the output much.

when n hidden layers use an activation like the sigmoid function, n smalJackie Chi Kit Cheung

l derivatives are multiplied together. Thus, the gradient decreases exponentially as we propagate down to the initial layers.

Sigmoid vs Softmax

Softmax Function	Sigmoid Function
Used for multi-classification logistic regression model	Used for binary classification in logistic regression model
The probabilities sum will be 1	The probabilities sum need not be 1
Used in the different layers of neural networks	Used as activation function while building neural networks
The high value will have the higher probability than other values	The high value will have the high probability but not the higher probability

Overfitting

Def: While training the model, you can observe some high accuracy and some low accuracy so you have high variance

Dropout Regularization

During training, some number of layer outputs are randomly ignored or “dropped out.”

Question: Where should I place dropout layers in a neural network?

In the original paper that proposed dropout layers, by Hinton (2012), dropout (with p=0.5) was used on each of the fully connected (dense) layers before the output; it was not used on the convolutional layers. This became the most commonly used configuration.

More recent research has shown some value in applying dropout also to convolutional layers, although at much lower levels: p=0.1 or 0.2. Dropout was used after the activation function of each convolutional layer: CONV->RELU->DROP.

One-hot encoding in classifier

MSE VS CROSS-ENTROPY

In softmax classifier, why use exp function to do normalization?

Because we use the natural exponential, we hugely increase the probability of the biggest score and decrease the probability of the lower scores when compared with standard normalization. Hence the “max” in softmax.

DL Principles

"Tower relies on its foundation"