“To strive, to seek, to find, and not to yield”
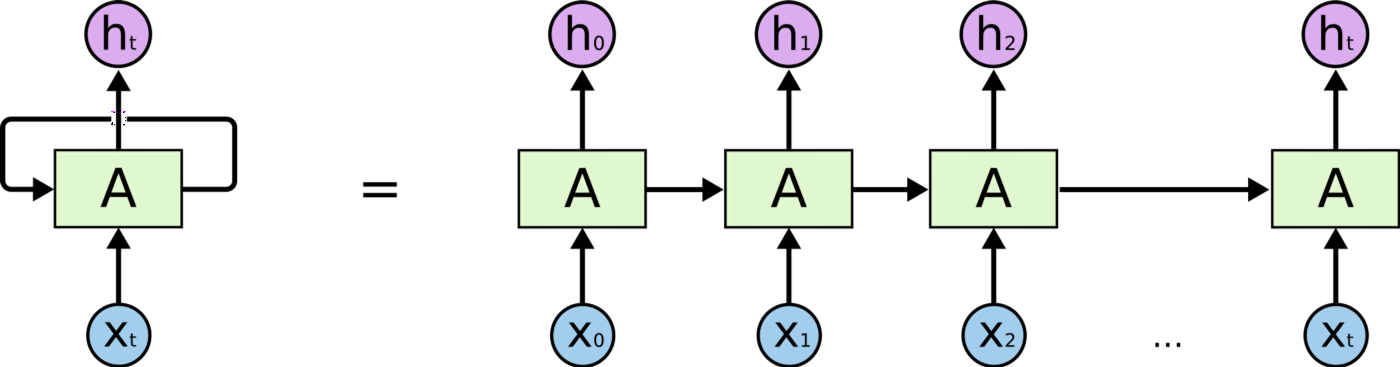
RNN is mainly used in the scenario of there is a need to remember the past information and pass propagate to the future. Variants of RNN eliminate its structural deficiency.
RNN (Recurrent Neural Network)
GIF LSTM&RNN Procedure YouTube
Short-term memory dependency, not capable for long-term memory
The Vanishing Gradient Problem In RNN
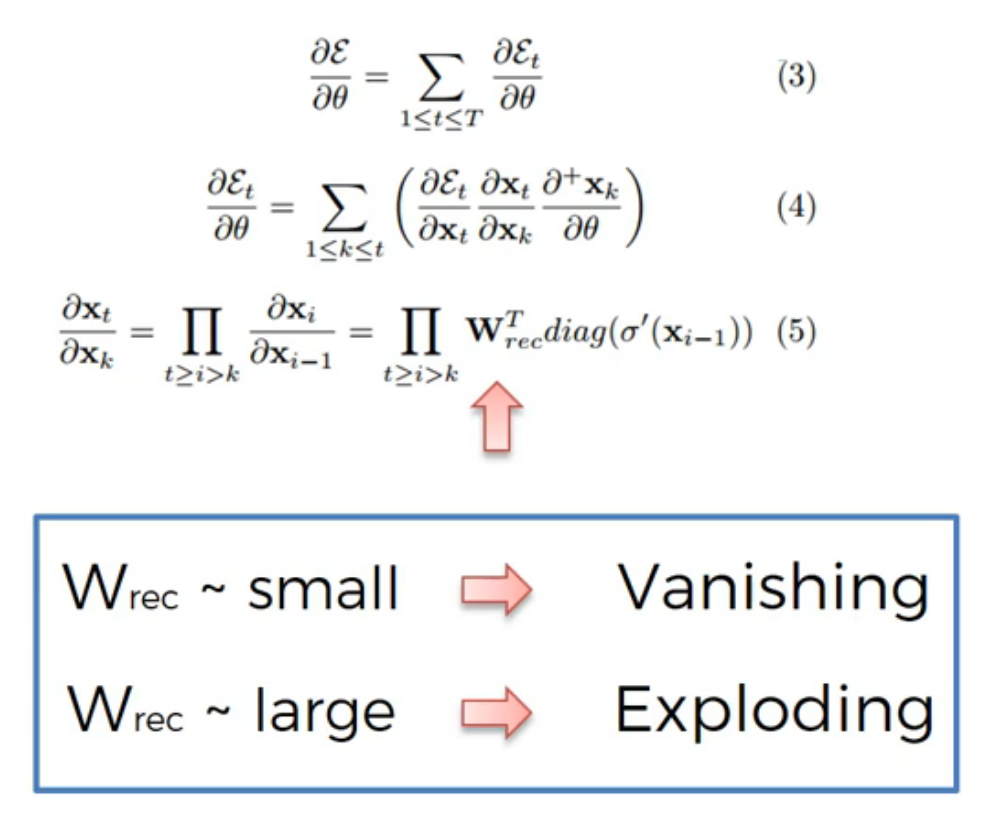
Weights are assigned at the start of the neural network with the random values, which are close to zero, and from there the network trains them up. But, when you start with wrec close to zero and multiply xt, xt-1, xt-2, xt-3, … by this value, your gradient becomes less and less with each multiplication.
** Gradient Vanishing is easy to appear in RNN because when the gradient is passed backwards, because the same matrix is multiplied too many times, the gradient tends to gradually disappear, resulting in the subsequent nodes cannot update the parameters, and the entire learning process cannot be performed appropriately**
Why
This arrow means that long-term information has to sequentially travel through all cells before getting to the present processing cell. This means it can be easily corrupted by being multiplied many time by small numbers < 0. This is the cause of vanishing gradients.
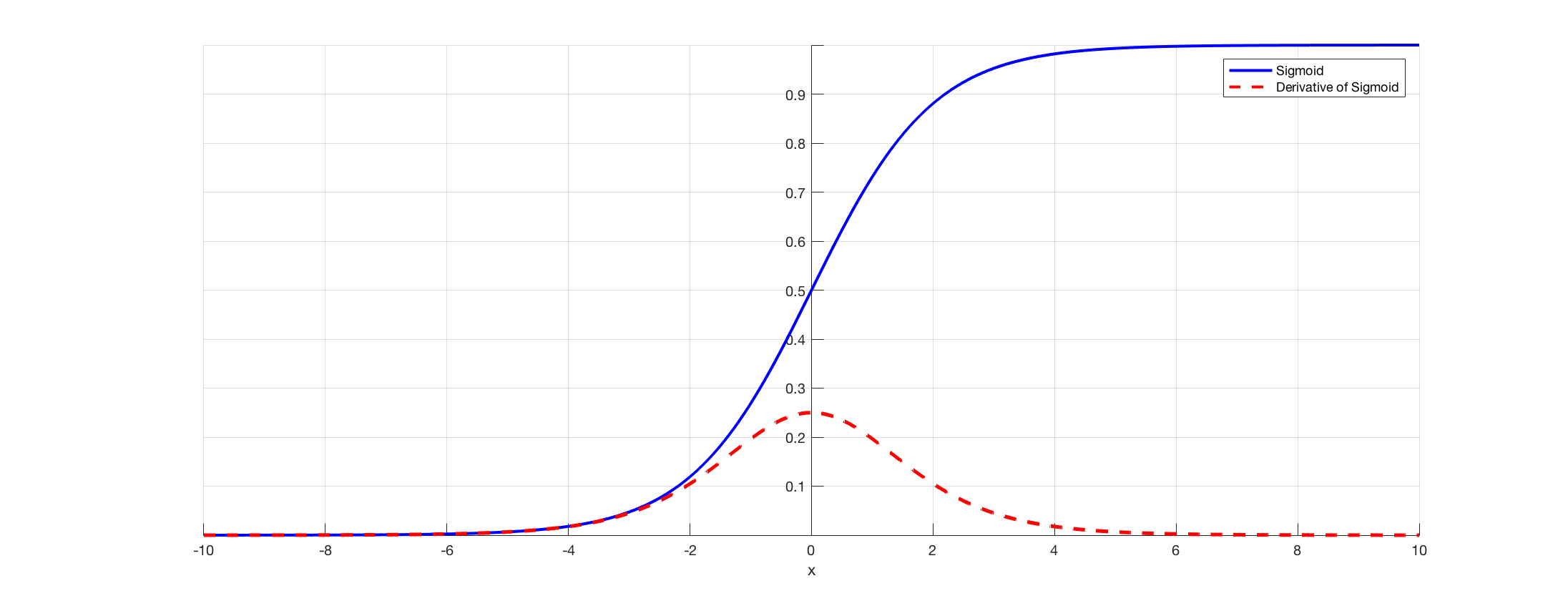
!!! For example: these two are the common-used activation functions in RNN
Sigmoid as activation function
Tanh as activation function
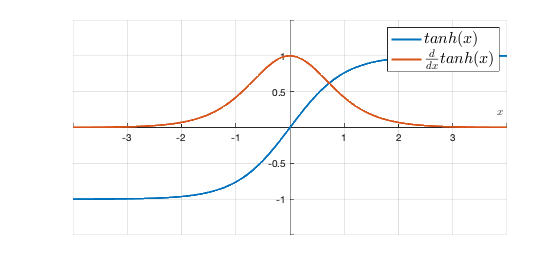
When backpropagating, the partial derivative of tanh or sigmoid activation function will restrict itself between 0-1, 0-0.25, correspondingly, if the Weight < 4 => dev_sigmoid’* W < 1, so the multiplication/chain rule of these function values will go to 0 as more and more layers in the network.
****
More details:

Problem
If a change in the parameter’s value causes very small change in the network’s output - the network just can’t learn the parameter effectively, which is a problem. (the gradients of the network’s output with respect to the parameters in the early layers become extremely small)
Cause
Vanishing gradient problem depends on the choice of the activation function. Many common activation functions (e.g sigmoid or tanh) ‘squash’ their input into a very small output range in a very non-linear fashion. For example, sigmoid maps the real number line onto a “small” range of [0, 1], especially with the function being very flat on most of the number-line. As a result, there are large regions of the input space which are mapped to an extremely small range. In these regions of the input space, even a large change in the input will produce a small change in the output- hence the gradient is small.
This becomes much worse when we stack multiple layers of such non-linearities on top of each other. For instance, first layer will map a large input region to a smaller output region, which will be mapped to an even smaller region by the second layer, which will be mapped to an even smaller region by the third layer and so on. As a result, even a large change in the parameters of the first layer doesn’t change the output much.
We can avoid this problem by using activation functions which don’t have this property of ‘squashing’ the input space into a small region. A popular choice is Rectified Linear Unit which maps xx to max(0,x)max(0,x).
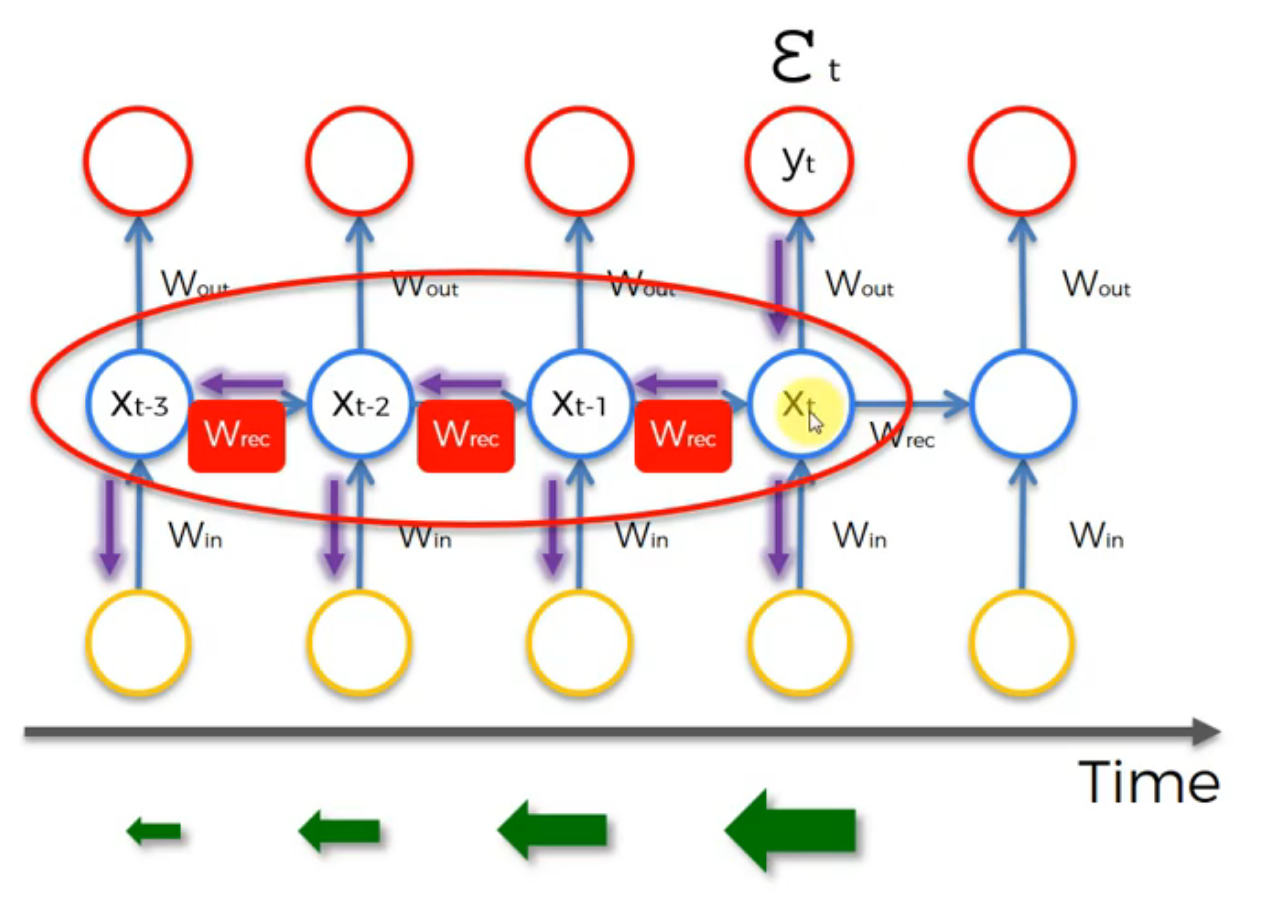
While backproporgating, the weights are getting smaller as shows above will cause the gradient small, training slow and even model will not be able to trained properly.
Solution
- Exploding Gradient
- Truncated Backpropagation (step BP after a certain point; that’s probably not optimal because then you’re not updating all the weights; if you don’t stop, then you’re just going to have a completely irrelevant network.)
- Penalties (penalize gradient)
- Gradient Clipping (have a maximum limit for the gradient.)
- Vanishing Gradient
- Weight Initialization (initialize your weights to minimize the potential for vanishing gradient.)
- Echo State Networks
- LSTM
-
Previous
CNN Architecture Explain and Why it Works -
Next
Why LSTM Solves the Gradient Vanishing Problem of RNN