Boosting vs Bagging
Bagging (bootstrap aggregating)
Bagging is the bagging method, and its algorithm is as follows:
A) Extract the training set from the original sample set. In each round, n training samples are extracted from the original sample set using Bootstrapping (in the training set, some samples may be drawn multiple times, with replacement and some samples may never be drawn). A total of k rounds of extraction are performed to obtain k training sets. (The k training sets are independent of each other)
B) Use one training set at a time to get one model, and k training sets get a total of k models. (Note: There is no specific classification algorithm or regression method here, we can use different classification or regression methods according to specific problems, such as decision trees, perceptrons, etc.)
C) For the classification problem: the k models obtained in the previous step are used to obtain the classification results by voting; for the regression problem, the average value of the above models is calculated as the final result. (All models have the same importance)
Boosting
The main idea is to assemble the weak classifier into a strong classifier. Under the PAC (probability approximate correct) learning framework, the weak classifier can be assembled into a strong classifier.
Two core questions about Boosting:
1) How to change the weight or probability distribution of training data in each round?
By increasing the weights of the samples that were misclassified classified by the weak classifier in the previous round and reducing the weights of the samples that were correctly classified in the previous round, the classifier will have a better effect on the misclassified data.
2) What methods are used to combine weak classifiers?
The weak classifiers are combined linearly through the additive model. For example, AdaBoost uses weighted majority voting, to increase the weight of classifiers with smaller error rates, while reducing the weight of classifiers with larger error rates.
By gradually reducing the tree’s fitting residual error, the model generated at each step is ensembled to obtain the final model.
The difference between Bagging and Boosting
1) Sample selection:
Bagging: The training set is selected with replacement from the original set, and each round of the training set selected from the original set is independent.
Boosting: The training set of each round remains unchanged, but the weight of each sample in the training set in the classifier changes. The weights are adjusted according to the classification results of the previous round.
2) Sample weights during training:
Bagging: Use uniform sampling, each sample has equal weight
Boosting: The weights of the samples are continuously adjusted according to the error rate. The greater the error rate, the greater the weight. (greater weights with higher misclassifications)
3) Prediction function:
Bagging: All prediction functions have equal weight.
Boosting: Each weak classifier has a corresponding weight. At the end of voting, a classifier with a small classification error will have a greater weight.
4) Parallel computing:
Bagging: Each prediction function can be generated in parallel
Boosting: Each prediction function can only be generated sequentially, because the latter model parameters require the results of the previous round of models.
Bootstrap
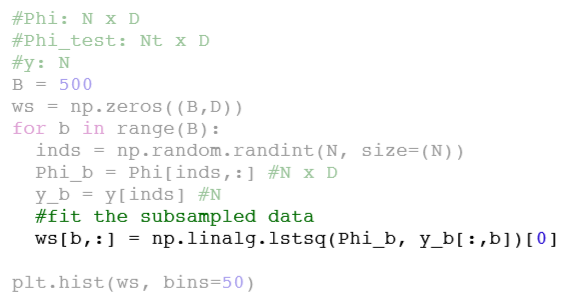
Codes
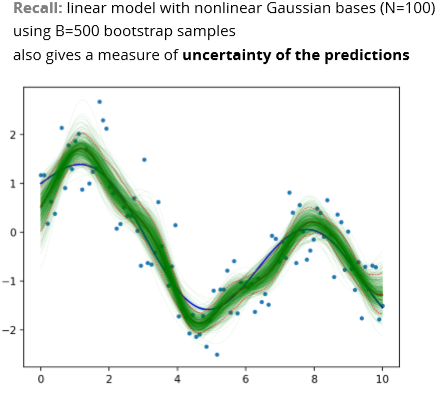
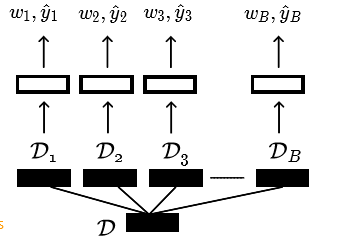
Bagging (Bootstrap aggregating)
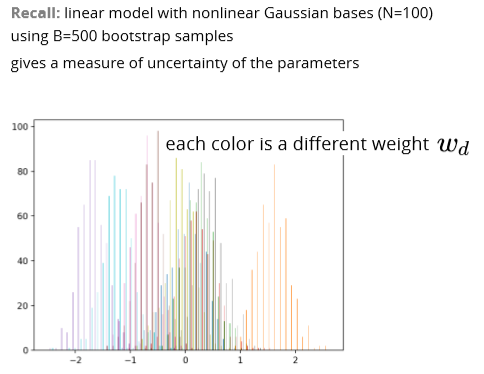
Use bootstrap for more accurate prediction (not just uncertainty)
Bagging for regression
Will lower variance but same bias
Bagging for classification
mode of iid classifiers that are better than chance is a better classifier
- use voting
crowds are wiser when
- individuals are better than random
- votes are uncorrelated
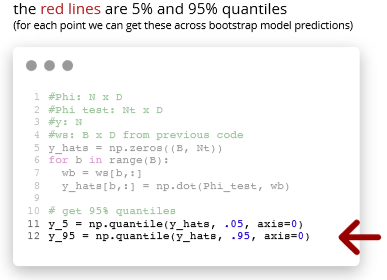
Example
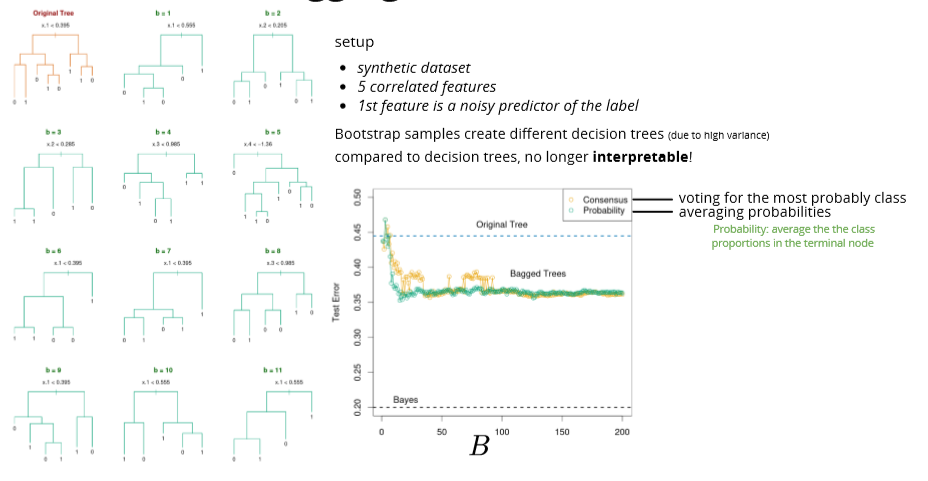
Random forests
Reduce the correlation between decision trees
Feature sub-sampling
only a random subset (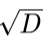
) of features are available for split at each step (further reduce the dependence between decision trees)
Features of Random Forest
- It is unexcelled in accuracy among current algorithms.
- It runs efficiently on large data bases.
- It can handle thousands of input variables without variable deletion.
- It gives estimates of what variables are important in the classification.
- It generates an internal unbiased estimate of the generalization error as the forest building progresses.
- It has an effective method for estimating missing data and maintains accuracy when a large proportion of the data are missing.
- It has methods for balancing error in class population unbalanced data sets.
- Generated forests can be saved for future use on other data.
- Prototypes are computed that give information about the relation between the variables and the classification.
- It computes proximities between pairs of cases that can be used in clustering, locating outliers, or (by scaling) give interesting views of the data.
- The capabilities of the above can be extended to unlabeled data, leading to unsupervised clustering, data views and outlier detection.
- It offers an experimental method for detecting variable interactions
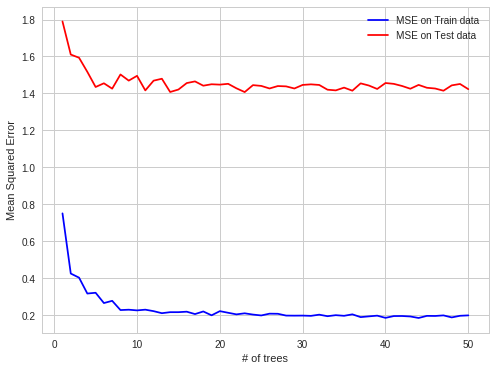
Random forest does not overfit because each tree is independent and starts from scratch and Random Forest takes the average of all the predictions, which makes the biases cancel each other out. In general, more trees will be resulted in more stable generalization errors.
formula prove:
****
Out of bag (OOB) samples
- the instances not included in a bootstrap dataset can be used for validation
- simultaneous validation of decision trees in a forest
- no need to set aside data for cross validation
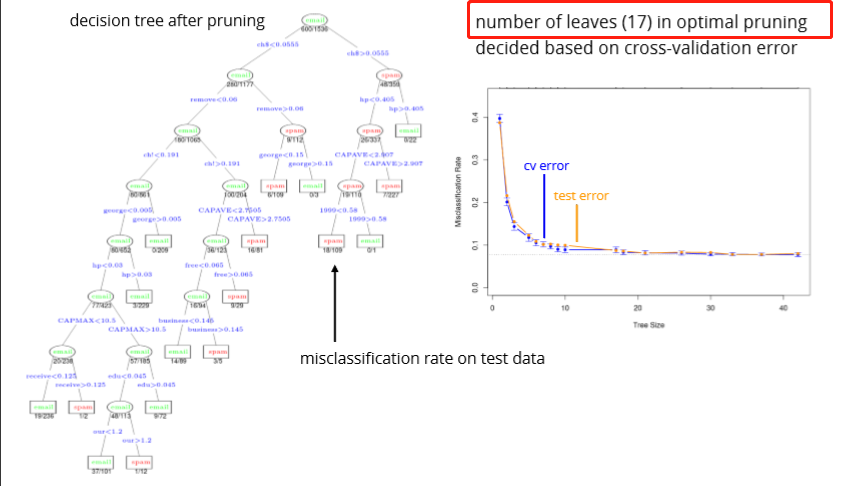
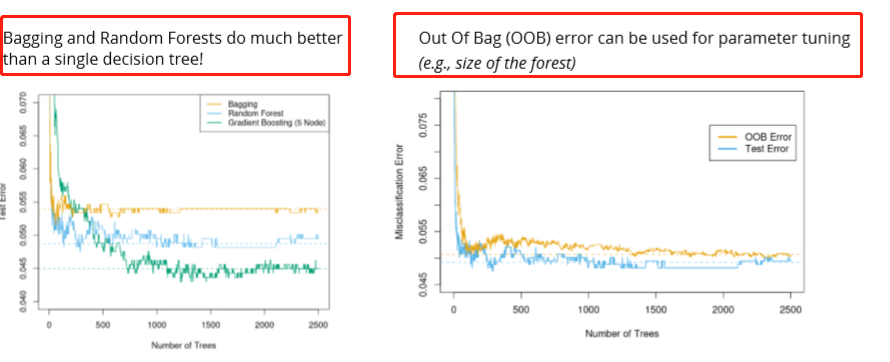
Out Of Bag (OOB) error can be used for parameter tuning (e.g., size of the forest)
Summary
- Bootstrap is a powerful technique to get uncertainty estimates
- Bootstrap aggregation (Bagging) can reduce the variance of unstable models
- Random forests (subsample data and features):
- Bagging + further de-correlation of features at each split
- OOB validation instead of CV
- destroy interpretability of decision trees
- perform well in practice
- can fail if only few relevant features exist (due to feature-sampling)
Adaptive bases
Optimization idea
Example
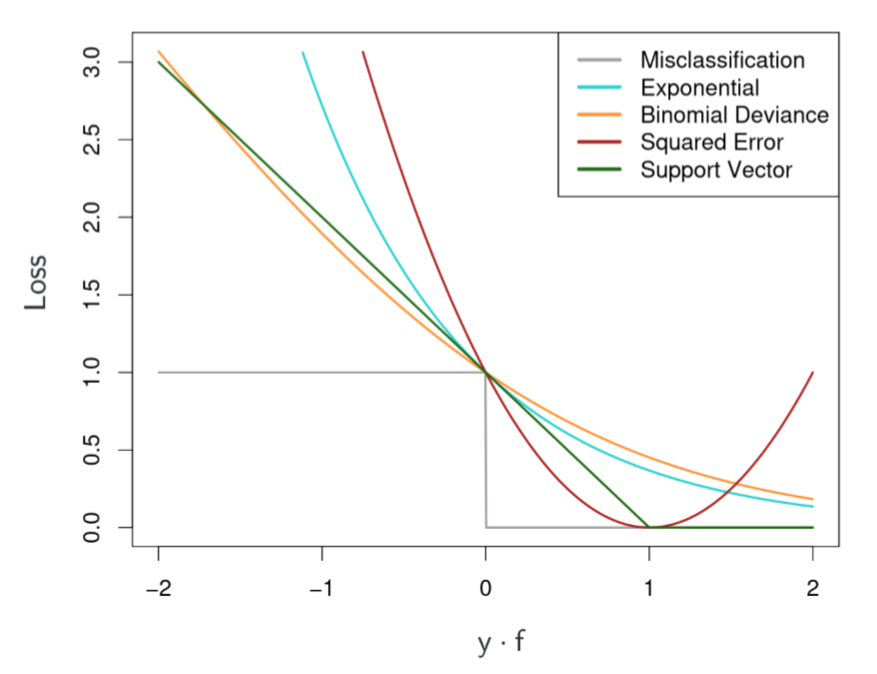
Exponential loss
note that the loss grows faster than the other surrogate losses (more sensitive to outliers)
AdaBoost
AdaBoost algorithm
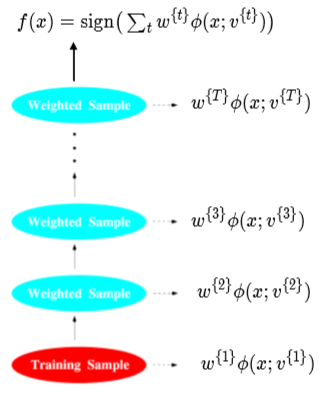
AdaBoost detailed derivations
Discrete AdaBoost
Discrete AdaBoost Algorithm Example
Example
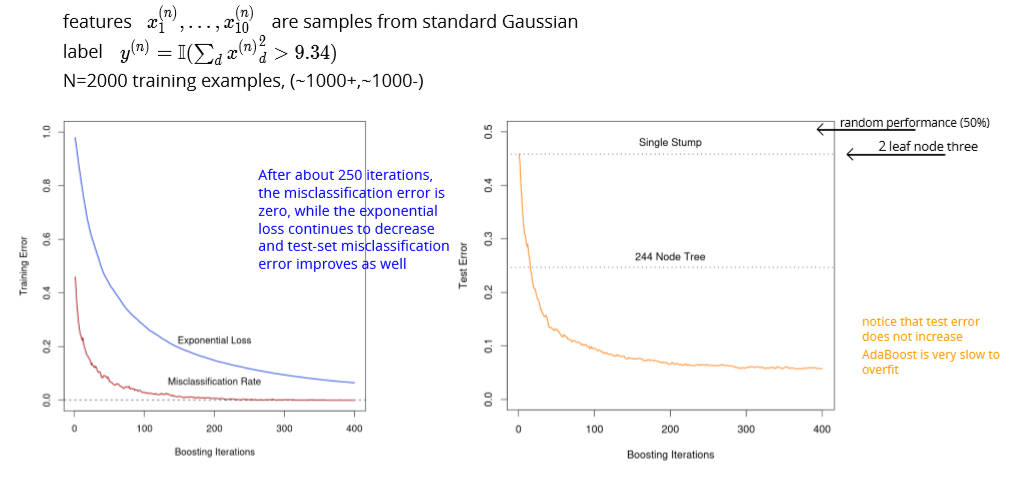
Decision stump: decision tree with one node
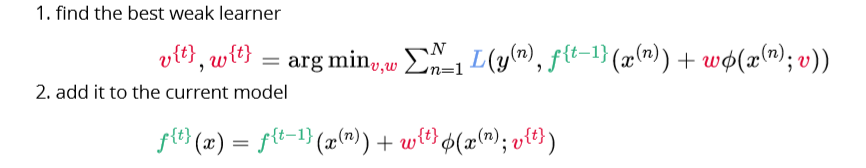
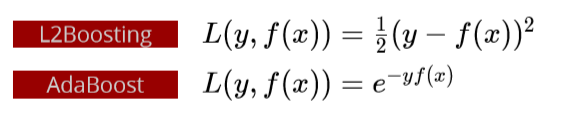
Gradient boosting
Algorithm
Gradient tree boosting
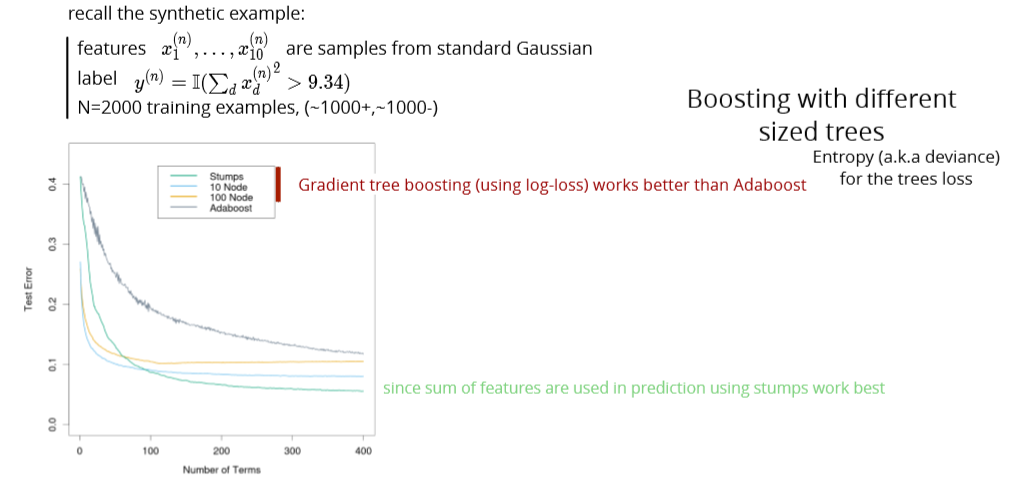
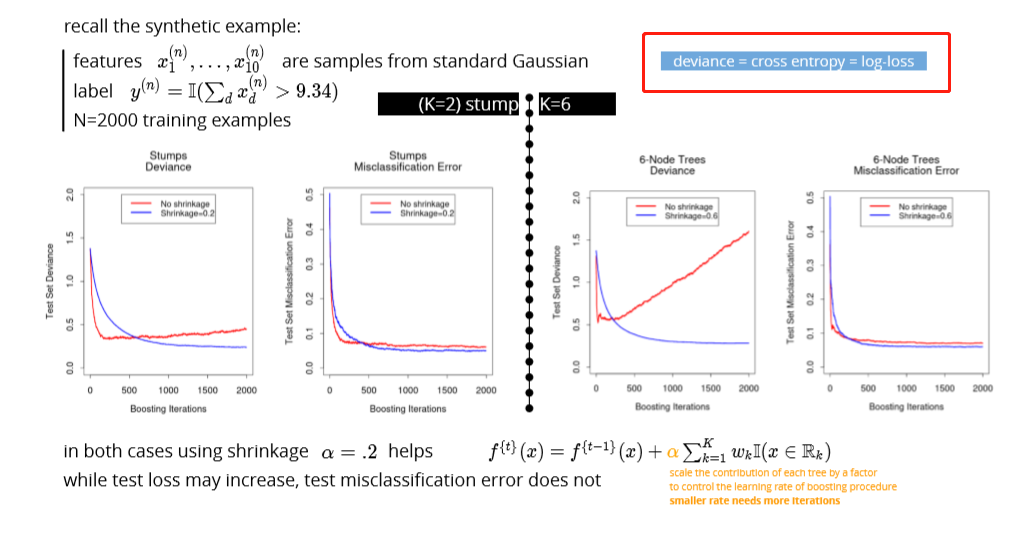
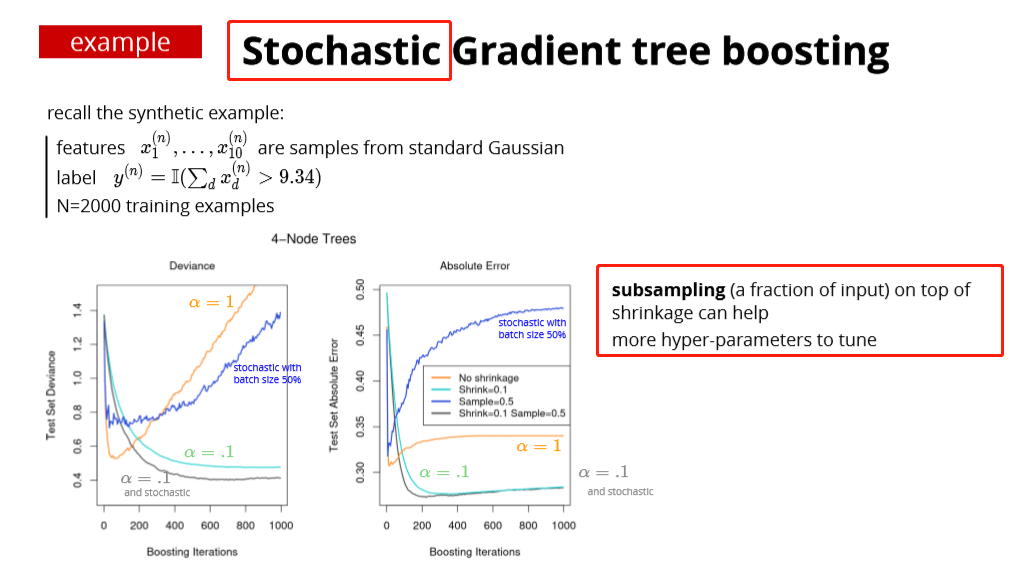
two ensemble methods
- bagging & random forests (reduce variance)
- produce models with minimal correlation
- use their average prediction
- boosting (reduces the bias of the weak learner)
- models are added in steps
- a single cost function is minimized
- for exponential loss: interpret as re-weighting the instance (AdaBoost)
- gradient boosting: fit the weak learner to the negative of the gradient
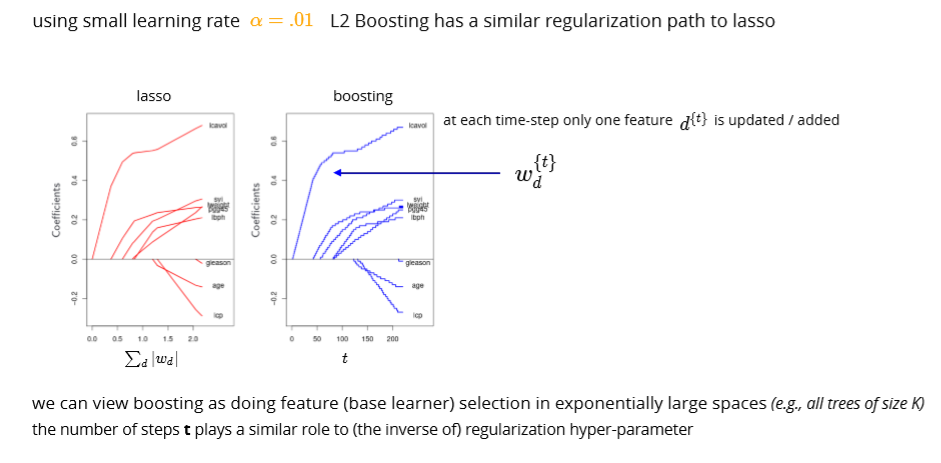
- interpretation as L1 regularization for “weak learner”-selection
- also related to max-margin classification (for large number of steps T)
- random forests and (gradient) boosting generally perform very well
Some loss functions for gradient boosting
Maximum Likelihood Estimation
- given a pdf
the pdf w.r.t X- Log step 2
- Get the derivate = 0 w.r.t the estimator you would like to
- Get the MLE w.r.t the estimator
pg. 4
